Math and Dynamics

Czech technical University in Prague
Faculty of Information Technology
Department of Software Engineering
© Adam Vesecký, MI-APH, 2019

Literature

Verth, Van. 2008. Essential Mathematics for Games and Interactive Applications

Randomness

Generative algorithms

  • Random functions
  • Noise functions
  • Fractals

Randomness in games

Randomness is one of the most critical factors in ensuring an engaging game. Random events turn the game into a strict uncertainty, causing players to analyze the opportunity costs of their choices.

Random generator methods

LCRNG

  • Linear Congruential Random Number Generator
  • starts with a seed value and performs some arithmetic operations which is both returned and used to reseed the generator
  • works best with prime values
  • chosen well, they won't cycle until they nearly exhaust their domain
  • used in rand() from standard C library

Lagged Fibonacci methods

  • we are looking further back into the sequence of values

Carry methods

  • takes part of the result from the previous stage and carries it forward to the least
    significant bits in the next stage

Random number generators

Mersenne Twister

  • introduced in 1997
  • colossal period of 2^19937-1
  • passes Diehard test
  • uses SIMD vector instructions

Mother of all

  • introduced in 1992
  • multiply-with-carry technique
  • adds the high-entropy bits to the low-entropy bits
  • faster than twister, period of 2^250

Xoroshiro128+

  • improved MOA, faster but less random
  • used in many browsers for Math.random()

Random functions distribution

Doom

Transport Tycoon

Lehmer RNG

Gaussian MOA

Xorshift

Random functions distribution

Uniform distribution

  • most common distribution of random generators
  • applications: noise, shuffling, one-of-many selection

Gaussian (normal) distribution

  • more common in games - every characteristic has some kind of average, with individuals varying with a normal distribution
  • can be calculated from a uniform generator via transformation (Box-muller algorithm)
  • applications: height of trees, aiming for projectiles, average speed, physical reaction time, reload rate, refresh healing rate, critical hit

Uniform distribution

Gaussian distribution

Terms

Seed

  • a hash that initializes random generators
  • a good source of entropy is user input or current time

Loot

  • items obtained over the gameplay (money, spells, equipment, weapons,...)

Spinning

  • calling the random function on a time-frame basis without using the result
  • advances the game to a difficult-to-predict place

Rarity slotting

  • a method of standardization to determine rates (common, rare, epic, legendary)
  • makes game events occur proportionally
  • can be defined as a rarity table, calculated via weighted sum

Random encounter

  • popular mechanics of RPG games (Final Fantasy, WoW, Pokémon, Golden Sun)
  • the game suddenly shifts to battle mode, forcing the player to fight
  • after winning the battle, the player receives a reward (skill upgrade, items, money)

Randomness in games

Final Fantasy 1 (1987)

  • reading sequentially from a list of pre-generated numbers (256 values in ROM)
  • we could encounter the same group of enemies - surprise determination

Super Mario 64 (1996)

  • used LCRNG with 65114 possible states
  • no spinning, the algorithm cycles only during certain events

Pokémon series for GBA (2002)

  • in Ruby/Diamond/Emerald, the RNG is spun every frame
  • Emerald sets the seed to zero on power-up
  • knowing which frame generates a shiny Pokémon can cut down on the work
    needed to get it (otherwise it's 1:8192 prob)

Darkwing Duck (in the picture)

  • delaying a frame causes a different drop

Randomness in games

Pitfall!

Pitfall! (1982)

  • used linear-feedback shift register
  • every screen is defined by 1 byte - 256 screens in total
  • e.g. if a certain bit is 1, there is a water in the level

Doom (1993)

  • the worst pseudo-random number generator ever
  • a list of 256 random numbers cycled through

Diablo 1 (1996)

  • fully procedural levels
  • several stages - determine walkable paths, combine pre-authored chunks, fix faults by minisets

XCOM: Enemy Unknown (2012)

  • no random spinning - dangerous when saving the game before taking an important shot

No Man's Sky (2016)

  • gussied-up version of Pitfall!
  • very little data is stored on the game's servers as all elements of the game are created through deterministic algorithms and random number generators from a 64-bit seed

Example: Random number table in Doom

unsigned char rndtable[256] = {

      0,   8, 109, 220, 222, 241, 149, 107,  75, 248, 254, 140,  16,  66 ,

     74,  21, 211,  47,  80, 242, 154,  27, 205, 128, 161,  89,  77,  36 ,

     95, 110,  85,  48, 212, 140, 211, 249,  22,  79, 200,  50,  28, 188 ,

     52, 140, 202, 120,  68, 145,  62,  70, 184, 190,  91, 197, 152, 224 ,

    149, 104,  25, 178, 252, 182, 202, 182, 141, 197,   4,  81, 181, 242 ,

    145,  42,  39, 227, 156, 198, 225, 193, 219,  93, 122, 175, 249,   0 ,

    175, 143,  70, 239,  46, 246, 163,  53, 163, 109, 168, 135,   2, 235 ,

     25,  92,  20, 145, 138,  77,  69, 166,  78, 176, 173, 212, 166, 113 ,

     94, 161,  41,  50, 239,  49, 111, 164,  70,  60,   2,  37, 171,  75 ,

    136, 156,  11,  56,  42, 146, 138, 229,  73, 146,  77,  61,  98, 196 ,

    135, 106,  63, 197, 195,  86,  96, 203, 113, 101, 170, 247, 181, 113 ,

     80, 250, 108,   7, 255, 237, 129, 226,  79, 107, 112, 166, 103, 241 ,

     24, 223, 239, 120, 198,  58,  60,  82, 128,   3, 184,  66, 143, 224 ,

    145, 224,  81, 206, 163,  45,  63,  90, 168, 114,  59,  33, 159,  95 ,

     28, 139, 123,  98, 125, 196,  15,  70, 194, 253,  54,  14, 109, 226 ,

     71,  17, 161,  93, 186,  87, 244, 138,  20,  52, 123, 251,  26,  36 ,

     17,  46,  52, 231, 232,  76,  31, 221,  84,  37, 216, 165, 212, 106 ,

    197, 242,  98,  43,  39, 175, 254, 145, 190,  84, 118, 222, 187, 136 ,

    120, 163, 236, 249

};

 

int P_Random (void) {

    prndindex = (prndindex+1)&0xff;

    return rndtable[prndindex];

}

Noise

  • Randomness is used to vary characteristics, noise is used to vary them over time or in space
  • Noise functions
    • Lattice-based
      • Perlin Noise, Simplex Noise, Wavelet noise, Value noise
    • Point-based
      • Worley noise (Voronoi/Cellular)

Perlin Noise

  • Perlin Noise - developed by Ken Perlin in 1983
  • Simplex Noise - Perlin's improved noise, fewer artifacts and lower computational overhead
  • both are gradient noises - we set a pseudo-random gradient at regularly spaced points in space and interpolate between them
  • the noise is constructed from octaves (contribution to the signal at a particular scale)
  • the signal is interpolated via a quartic function:

float PerlinNoise2D(int x, int y, float persistence, int octaves, float zoom) {

    float total = 0.0f;

    // initial frequency and amplitude

    float frequency = zoom;

    float amplitude = 1.0f;

 

    for (int i = 0; i < octaves; i++) {

        // calculate noise

        total = total + InterpolatedNoise(x*frequency, y*frequency) * amplitude;

        // update frequency and amplitude

        frequency = frequency * 2;

        amplitude = amplitude * persistence;

    }

    return total; }

Perlin noise example

1 octave

2 octaves

4 octaves

8 octaves

persist. 0.2

persist. 0.4

persist. 0.6

persist. 0.8

Fractals

  • discovered in 1975
  • rough or fragmented geometric shapes that can be subdivided in parts, each of which is a reduced-size copy of the whole
  • used for creating procedural textures and visual effects

Data structures

Data structures cheatsheet

Spatial Partitioning

Oct-tree

Bounding volume

  • groups objects or their parts together based on their positions and sizes
  • if the object moves, so will the hierarchy
  • used for physics, shape analysis, precise collision detection

Spatial data structure

  • a structure that stores objects by their position
  • is locked to the world
  • used for range queries, neighborhood searching, rough collision detection
  • the more objects we have, the more benefits we get
  • Implementations
    • BSP - binary-space partitioning
    • Quad-tree - for 2D and semi-3D space
    • Oct-tree - for 3D space
    • Grid - a square grid

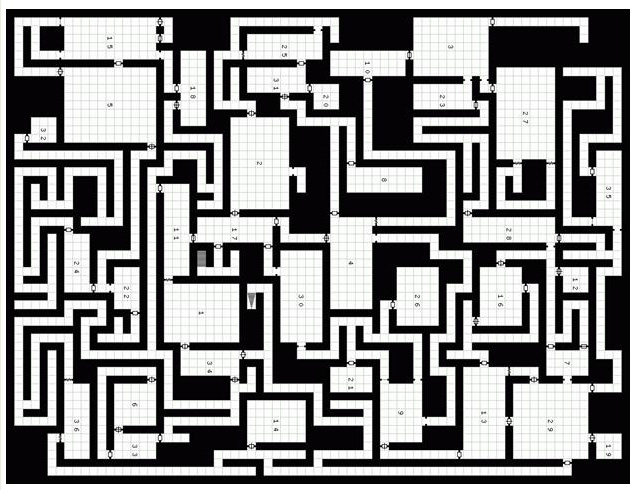
Binary space partitioning

  • algorithm that decomposes a polygon-soup into a tree that contains convex sets
  • it was first used in Doom to solve difficult rendering of circles around pillars
  • very good for rendering, ray-tracing and collision detection in complex indoor environments
  • works only in static environments and requires a complex preprocessing stage

Quad-tree

  • hierarchical partition
  • each inner node has 4 children
  • it is common to have the children of same size -> we won't need to save the position vector
  • overlapping objects are put it into all children they touch
  • only objects in the same leaf can be in collision
  • useful for outdoor scenes, where objects are placed on a landscape
  • good for a small amount of objects of various sizes

Quad-tree for geometric hashing

Quad-tree for bounding volumes

Oct-tree

  • doesn't need an expensive preprocessing stage
  • allows very complex level geometry and easy editing
  • used for LoD, collision detection, voxel graphics,...
  • 0 subdivisions - 1 node
  • 1 subdivision - 9 nodes
  • 2 full subdivisions - 73 nodes
  • 3 full subdivisions - 585 nodes

Grid

  • implemented as an array or a hash-table
  • each cell has a list of units that are inside
  • if a unit crosses the boundary of the cell, we need to move it to the other list
  • good for a large amount of objects of similar size
  • very fast to locate an object - in sharp contrast with recursing down a quad-tree
  • takes up more memory, granularity needs to be determined in advance
  • multi-resolution map
    • hybrid structure, uses multiple grids of different sizes
    • objects are added into one of the grids based on their size

Steering behaviors

Steering behaviors

  • set of algorithms and principles that help autonomous agents move in a realistic manner
    by using simple forces
  • designed by Craig Reynolds  in the early 90's
  • Agent - a system situated within an environment, having an ability to sense that environment
  • three layers of motion behavior:
    • action selection - choosing goals, strategy
    • steering - trajectory calculation
    • locomotion - way of moving, animation, articulation

Seek

  • the simplest steering behavior
  • a force that directs an agent toward a target position

Flee and arrive

Flee

  • opposite of seek
  • creates a force that steers the agent away

Arrive

  • seek is not good at stopping
  • arrive decelerates the agent onto the target position
  • additional parameter: slowing radius

Pursuit and Evade

Pursuit

  • agent intercepts a moving target
  • predicts where the target is going to be in the future
  • calls for a good prediction function

Evade

  • opposite of pursuite
  • the evader flees from the estimated future position

Wander

  • produces a force that will give an impression of a random walking
  • small random displacement is applied to the velocity vector every frame
  • a circle is projected in front of the vehicle
  • the vehicle is steered toward a target that moves along the perimeter
  • smoothness of movement depends on three parameters:
    • circle radius, distance from the vehicle and jittering (randomness)
  • the greater the radius and the distance, the stronger the force

Path follow

  • moves a vehicle along a set of waypoints
  • the last waypoint can be reached using arrive, the others via seek
  • smooth movement can be achieved using a tolerance radius or Bézier curve approximation
  • very sensitive to configuration (max force, max velocity, radius,...)

Obstacle avoidance and offset pursuit

Obstacle avoidance

  • steers a vehicle to avoid obstacles (usually approximated by a circle)
  • vehicle has a detection box - rectangular area
  • two forces are calculated: lateral force and braking force

Offset pursuit

  • keeps a vehicle positioned at a specified offset from a leader vehicle
  • useful for battle formations

Flocking

  • emergent behavior, more agents/vehicles are taken into consideration
  • combination of three aspects:
    • separation - steers a vehicle away from its neighborhood
    • alignment - keeps the vehicle's direction aligned with its neighbors
    • cohesion - moves a vehicle toward the center of mass of its neighbors

Dynamics

World size

Unit SizeUnit Example Upper Range [m]Upper Range area
100mSpace Ship 1.67 x 10^9Diameter of the Sun
1mCar1.67 x 10^7Asia
1cmCoin1.67 x 10^6Mexico
1mmFluid particle1.67 x 10^5Paris
100μmDust1.67 x 10^4Manhattan
  • diameter of the known universe:
  • the smallest theoretical structure:
  • 256b integer gives us values
  • IEEE 754 format stores 24b of resolution in the mantissa: range of
    • single precision, 32bit:
    • double precision, 64bit:
  • most games set their basic units as meter, making millimeter the smallest unit
  • range areas for 32bit numbers:

Map Size Comparison

IEEE 754 precision

  • a quarter of all 32bit numbers are in the range of , half of them in
  • from 8 388 608 to 16 777 216, the precision for 32b is 1

Points and Vectors

  • Cartesian coordinate system - by far the most common
  • other systems: cylindrical, spherical
  • in 2D engines, Y-axis is usually inverted

2D coordinate system

3D coordinate system

Points and Vectors

Vector addition and subtraction

Magnitude of a vector

  • Vector - a quantity that has both a magnitude and a direction
  • vector can be used to represent a point, provided that we fix the tail of the vector
    to the origin of the coordinate system
  • addition and subtraction
    • vector + vector = vector
    • vector - vector = vector
    • point + vector = point
    • point - point = vector
    • point + point = undefined

Points and Vectors

  • Magnitude
    • scalar representing the length of the vector
  • Normalization
    • a unit vector is a vector with a magnitude of one:
  • Normal vector
    • vector is normal to a surface if it is perpendicular to it
  • Dot product
  • Cross product
    • yields another vector that is perpendicular to two vectors

Example: Direction

  • We want to rotate the bottom ship toward the other one.
  1. We know
  2. Calculate
    - it's already normalized
  3. Calculate
  4. Normalize lookAt':

Example: Direction

  1. let
  • or just simply:

Lines

  • we have two points:  and will take one step in  direction for the second one:
  • subtracting both, we get a vector  with the same orientation
  • all scalar multiplies of this vector from  will generate points along the line
  • Example: closest point to a line
    • given , we need to find  closest to
    • we compute the difference vector , then we project this onto  to get

Terms

  • Kinematics - determines motion of objects without reference to forces
  • Dynamics - determines how objects interact under the influence of forces
  • Time - a continuous progress of events, measured in seconds
  • Mass - a scalar quantity measured in kilograms
  • Position - a point or an area occupied by an object
  • Velocity - the rate of change of distance over time
  • Acceleration - the rate of change of velocity over time
  • Force - an action exerted upon a body in order to change its state
Most engines use MKS units (meters, kilograms, seconds) and radians for angles

Dynamics

Linear Dynamics

  • we ignore all rotational effects
  • position can be described by a position vector
  • velocity:
  • acceleration:
  • net force:
  • Newton's second law:
  • linear momentum:

Angular dynamics

  • angular velocity:
  • angular acceleration:
  • torque: , torque caused by a force applied to a location
    • if we apply an off-center force to an object, we expect it to spin

Newton's laws

Lex I

  • A body will remain at rest or continue to move in a straight line at a constant speed unless acted upon by a force

Lex II

  • The acceleration of a body is proportional to the resultant force acting on the body and is in the same direction as the resultant force

Lex III

  • When one body exerts a force on a second body, the second body exerts an equal force with opposite direction on the first body

In most games, Newton's laws don't apply to trees

Motion

Projectile motion

Slope motion (no friction)

Motion

Mass-Spring Motion

  • Hook's Law:
    •  is the spring constant

Equations of motion

  • finding , given knowledge of
  • vertical motion under the influence of gravity
  • moving with variable acceleration
    • drag force:
    • a simple approximation to air friction (the faster we go, the greater the friction force)
    • how to handle this: derive a function for velocity
    • too difficult - with every change of any force, we would need to modify the simulation code
    • analytical solutions are almost never possible in game physics

Numerical integration

  • Conditions:
    • we know an initial value of the function:
    • we know the derivatives
    • we know the time interval
  • given , the problem is to find
  • we will start at  and take steps in time along the tangent, until we generate an approximation for
  • integration methods provide use with the possibility of approximation with different precision and complexity

Integration methods

Implicit methods

  • make use of quantities from the next time step
  • decrease energy from the system

Semi-implicit methods

  • combination of explicit and implicit methods
  • very stable

Explicit methods

  • make use of known quantities at each time step

Runge-Kutta family

  • Euler methods, midpoint methods, RK4,...

Verlet family

  • Regular Verlet
  • Leapfrog Verlet
  • Velocity Verlet

Euler integration

    • Explicit method

    Improved method

    Implicit method

  • cheap and easy to implement
  • high error and poor stability, depending directly on the time step

Verlet integration

  • used in molecular dynamics, useful in simulating small particles (cloth, rope, soft objects)
  • time invariant - we can run it forwards and then backwards, ending up in the same place

Regular Verlet

  • derived by adding two Taylor series expansions

Verlet leap-frog

  • method that tracks velocity, but at half a time step off from the position calculation

Velocity Verlet

  • most accurate, acceleration needs to be computed twice
  • advantages over Euler when dealing with multiple bodies

Dynamics in games

Lecture 6 Review

  • Generative algorithms: random functions, noise functions, fractals
    • Uniform distribution - noise, shuffling, one-of-many selections
    • Gaussian distribution - aiming for projectiles, average speed, reload rate
    • Terms: seed, loot, spinning, rarity slotting, random encounter
    • Perlin Noise: uses pseudo-random gradient over points in space and interpolates between them
  • Spatial partitioning structures: BSP, Quad-tree, Oct-tree, Grid
  • Steering behaviors: seek, flee, arrive, pursuite, evade, wander, path follow, obstacle avoidance, offset pursuit, flocking
  • Vector operations - magnitude, normalization, normal vector, dot product
  • Integration methods: euler integration, verlet integration

Goodbye quote

Kirov ReportingC&C, Red Alert 2